Code a Complete Binary Tree from Scratch

In C

In this article we will explore how to write some code to generate a binary tree of any structure from scratch. For the code.

Expectations from Reader:

• Familiarity with functions and loops in any programming language.

• Familiarity with binary trees.

• Wants to have some algorithmic fun.

There are many reasons to delve into such a task, and while this (probably) won’t ever be something you will “have” to write for a job, it can still be pretty neat for example as a self-exercise in programming, preparing for a school test or a technical job interview. You may want it for other reasons, but whatever your reasons may be, let’s get right into it.

We’ll be coding in C, but essentially using any other programming language is possible (think Python, C++, Java, etc.) and as long as you’re doing the same logic it should be fine.

I will focus on building a complete binary tree. That will be the interesting part. I’ll sum up what we’ve learned, and towards the end, I shall give some questions for further exploration. Let’s get started together.

By the end of this article you will have:

• Made some nice observations about binary trees.

• Applied some algorithmic thought.

• Practiced programming.

• The ability to generate complete binary trees.

• Realized that binary trees are cool to code!

If you enjoy this article, don’t forget to subscribe.

Building a Complete Binary Tree

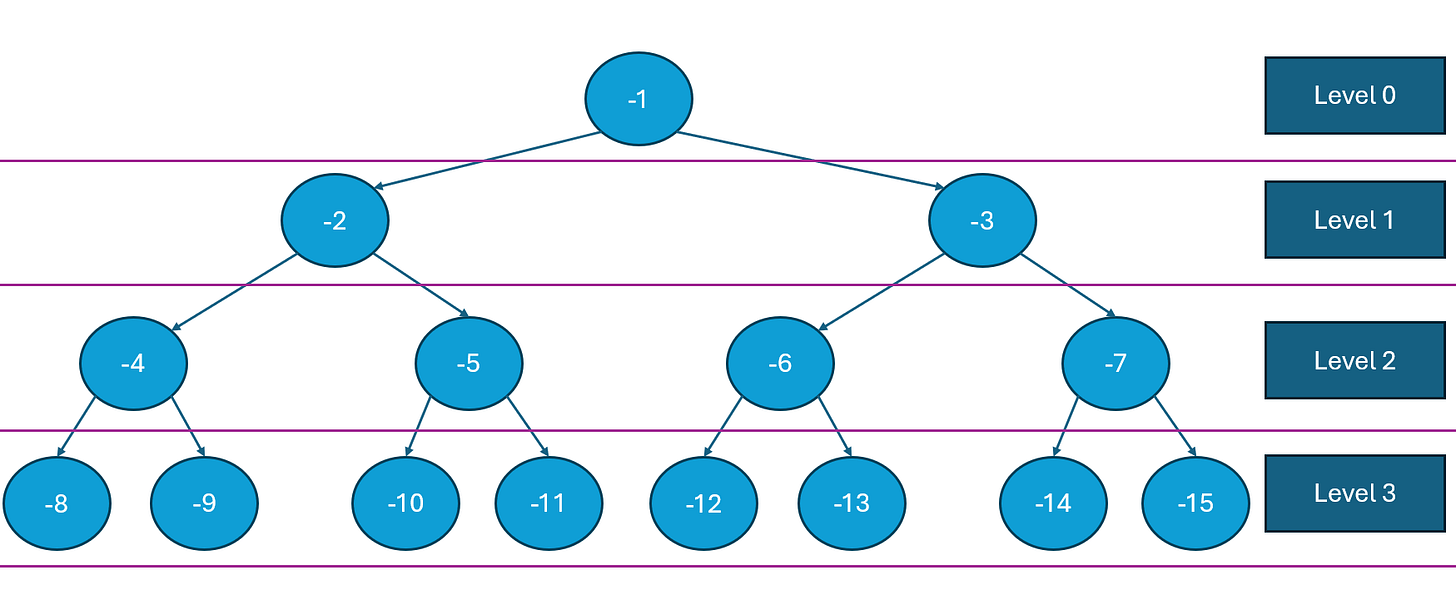
A complete binary tree, for the sake of this article, is a binary tree with an arbitrary number of levels, in which each level contains the maximum number of nodes.

For example, the following is a binary tree with four levels, Level 0 through 3:

Clearly, level 0 contains only the root node, and the final level (in the example level 3) will contain all the leaf nodes. No other level may contain a leaf node.

Moreover, observe this nice property: in any level i there are precisely 2^i nodes.
To see this, let us refer again to the example above:

We will be using precisely this property to generate each level.¹

Begin Coding

The full code is available on my Github. Feel free to snatch it and play with the code, but please refer to my Substack if you intend to use it.

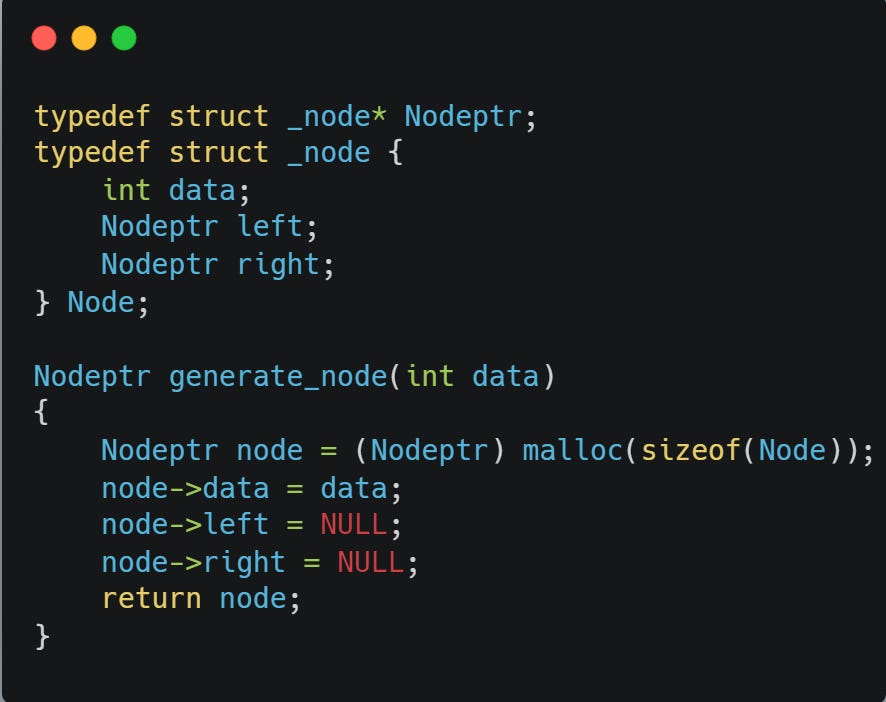
First, we’ll need some basic functionality to build nodes. So we define some structs (classes, in other programming languages) to represent a tree node. And build a function that generates those objects when called. So, add those in:²

If you’re not familiar with C and therefore unfamiliar with malloc, just know that it can generate as much memory as we ask of it.³

The main idea of our code will be to generate the tree level by level.
Next, we want to write some code which generates a new level, given the last (old) level. So, the next function’s signature is as follows:

In its’ parameters, it receives all the nodes of the last generated level as an array. The function returns a new array of nodes which are all the arrays of the next level (old_level + 1). A more illustrative example appears in the next section.

Building Just One Level

Notice, that the code for generate_node actually generates the leaves of the tree (because we set left=right=NULL); therefore, when we generate the final level, we need not worry about updating the left and right pointers of these nodes as they are already correctly instantiated. We will have to worry about updating the inner nodes’ left and right pointers. In other words, for all non-leaf nodes, we must change the contents of their left and right pointers from a NULL value to point to the correct node in the next level.

Imagine, we already have built Levels 0, 1, and 2 of the tree. Our task is now to build level 3 of the tree. Thus, we should call the function generateNewLevel with old_level set to 2. The function receives as parameters the orange array (Array Input in the image), and should return the green array (Array Output in the image):

Observe also, that the orange array’s nodes are now numbered 0 through 3, and the green array’s nodes are now numbered 0 through 7. These are actually the indices of these arrays.

Now observe these four similar observations:

• The orange node at index i=0 points with its left pointer at the green node at index 2*i=0, and with its right pointer at the green node at index 2*i+1=1.

• The orange node at index i=1 points with its left pointer at the green node at index 2*i=2, and with its right pointer at the green node at index 2*i+1=3.

• The orange node at index i=2 points with its left pointer at the green node at index 2*i=4, and with its right pointer at the green node at index 2*i+1=5.

• Can you guess where the left and right pointers of the orange node at index i=3 point to?

This will be true in the general case. Each node in the previous level at index i, should set its left to the new level at index 2*i and its right to the new level at index 2*i+1.

With these ideas, we are now ready to write the code of this function:

I hope along with the comments the function becomes self-explanatory.

Build the Entire Tree: Level By Level

The only thing left for us to do is to observe that we have a way to build a new level given a previous level. Therefore, if we build only the first level, we can simply call the function which we worked hard to write in order to generate all the next levels.

So we just need for someone to specify how many levels we should create. This next function receives the number of levels we must create as a parameter and returns the root node of the tree created:

The part which is harder to understand is probably the last loop: recall that generateNewLevel returns the array of the new level; thus, on the next iteration of the loop the returned levels are actually the old ones. This is why we both:

• Send old_level_nodes as a parameter to the function.

• And also rewrite it to be equal to the new level nodes, which are in fact, the *old* level nodes in the next iteration.

Testing

The next part is to make sure we succeeded. This will be easy if we are aware of the following two facts:

• First, an observation that we instantiated the tree like this (trace the code to be sure!):

• Second, given a binary tree, printing it pre-order, post-order and pre-order can generate only one and unique binary tree (in the structure sense).

The generated prints are:

which are the correct pre-order, in-order, and post-order printing respectively.

For the sake of completeness, I created the tree with the call
root = generateFullTree(4);

What have we learned?

Some new things you may have learned today:

• A nice indices trick to generate a complete binary tree.

• At least two Mathematical properties of trees.

• How to write nice, clean code to generate a complete binary tree.

• Coding can be fun.

• That I can’t write inline LateX within Substack.

If you are interested, I leave you with three, arguably interesting, challenges. Feel free to post your answers :)

A Minor Challenge

For those of you memory malloc nerds….

I’ve actually coded a lot of memory leaks. If interested, try to look for them and correct the code for me!

Time Complexity Challenge

If evaluating is your thing…

If we end up with n nodes, can you analyze the time complexity it takes us to build the tree in terms of n? Just for fun, if we generate k levels of the complete tree, how many nodes (n) are in the tree in terms of k?

What If I Wanted Other Trees?

Who says complete trees are the talk of town?

Can you take the current code and try to mitigate it to obtain any tree structure? Even better if you can mitigate it to any arbitrary tree structure without hurting the time complexity of our current work!

Feel free to leave your comments and ideas on how to solve these!

1. It will be nice to keep in mind that level i+1 has two times as many nodes as level i.

2. For simplicity, I added in the “int data” assuming the tree holds only integer data. This is easily generalized to any other type of data (e.g. floats, strings, or classes which represent data).

3. In C, malloc can be used to generate arrays of any type.